300. Longest Increasing Subsequence
2021. 11. 26. 15:56ㆍLeetcode
Description:
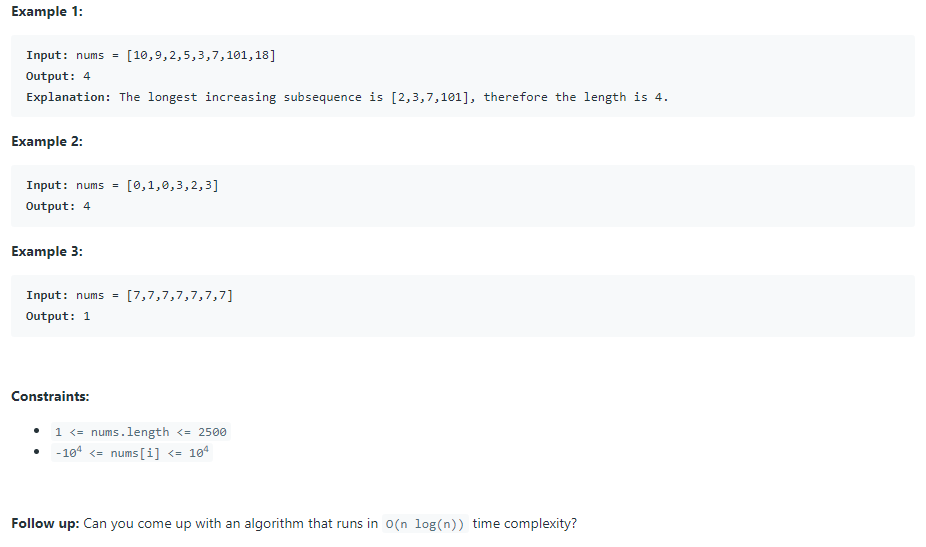
Given an integer array nums, return the length of the longest strictly increasing subsequence.
A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].
'''
[1] brute force)
-idea::
when, cur_num==-float(inf), from idx==0 to len(nums)-1, we can choice nums[idx] or not
consider all cases, and update longest
-code::
def bf(self, nums, i, cur_num, cur_len):
if i==len(nums):
self.longest=max(self.longest,cur_len)
return
# select
if nums[i] > cur_num:
self.bf(nums, i+1, nums[i], cur_len+1)
# not select
self.bf(nums, i+1, cur_num, cur_len)
def lengthOfLIS(self, nums: List[int]) -> int:
self.longest=0
self.bf(nums, 0, -float(inf), 0)
return self.longest
-T/C: O(2^n)
-S/C: O(n)
'''
'''
[2] dp)
-idea::
[10 9 2 5 3 7 101 8]
|
f(7) = max(f(2), f(5), f(3))+ 1 ** f(2), f(5), f(3) ==> smaller than 7
generally, f(i) = max( f(smaller than nums[i]), ... ) + 1
-code::
def lengthOfLIS(self, nums: List[int]) -> int:
max_len=1
dp=[ 1 for _ in range(len(nums))]
for i in range(1,len(nums)):
for j in range(0,i):
if nums[j] < nums[i]:
dp[i]=max(dp[i], dp[j]+1)
max_len=max(max_len, dp[i])
return max_len
-T/C: O(n^2)
-S/C: O(n)
'''
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
max_len=1
dp=[ 1 for _ in range(len(nums))]
for i in range(1,len(nums)):
for j in range(0,i):
if nums[j] < nums[i]:
dp[i]=max(dp[i], dp[j]+1)
max_len=max(max_len, dp[i])
return max_len'Leetcode' 카테고리의 다른 글
| 435. Non-overlapping Intervals (0) | 2021.11.21 |
|---|---|
| 57. Insert Interval (0) | 2021.11.21 |
| 106. Construct Binary Tree from Inorder and Postorder Traversal (0) | 2021.11.21 |
| 540. Single Element in a Sorted Array (0) | 2021.11.20 |
| 208. Implement Trie (Prefix Tree) (0) | 2021.11.17 |