106. Construct Binary Tree from Inorder and Postorder Traversal
2021. 11. 21. 21:55ㆍLeetcode
Description:
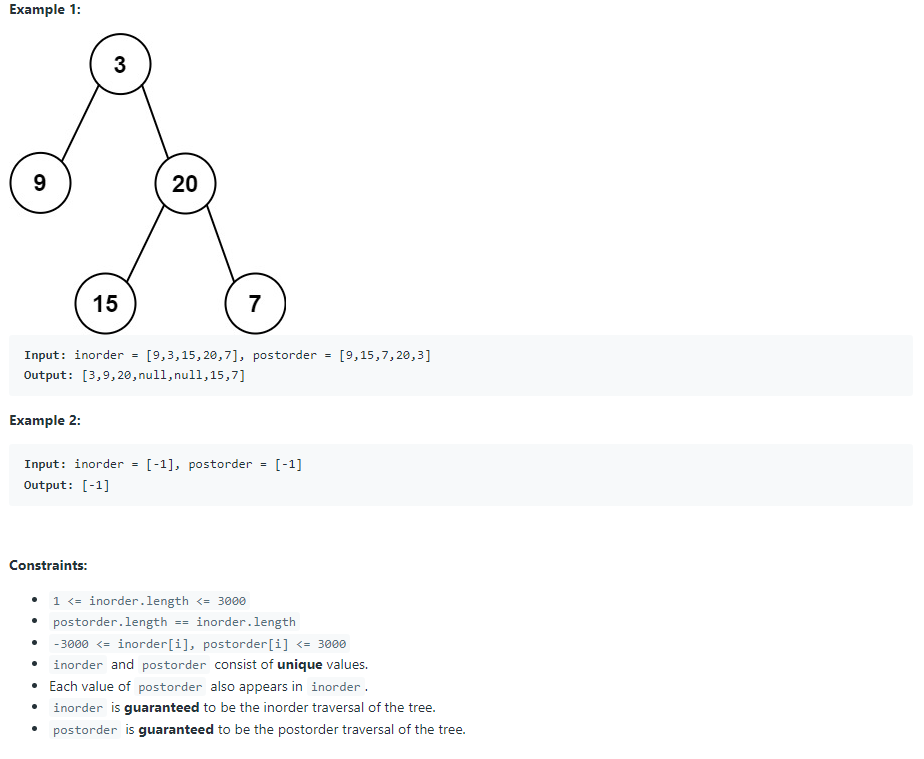
Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
'''
[1] divide and set)
-code::
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
if len(inorder)==0:
return None
# set root
root=TreeNode(postorder[-1])
# get root_idx in inorder
root_idx=inorder.index(root.val)
# set left and right
root.left=self.buildTree(inorder[0:root_idx],postorder[0:root_idx])
root.right=self.buildTree(inorder[root_idx+1:],postorder[root_idx:-1])
return root
-T/C: O(nlogn)
-S/C: O(logn)
'''
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
if len(inorder)==0:
return None
# set root
root=TreeNode(postorder[-1])
# get root_idx in inorder
root_idx=inorder.index(root.val)
# set left and right
root.left=self.buildTree(inorder[0:root_idx],postorder[0:root_idx])
root.right=self.buildTree(inorder[root_idx+1:],postorder[root_idx:-1])
return root'Leetcode' 카테고리의 다른 글
| 435. Non-overlapping Intervals (0) | 2021.11.21 |
|---|---|
| 57. Insert Interval (0) | 2021.11.21 |
| 540. Single Element in a Sorted Array (0) | 2021.11.20 |
| 208. Implement Trie (Prefix Tree) (0) | 2021.11.17 |
| 235. Lowest Common Ancestor of a Binary Search Tree (0) | 2021.11.17 |