647. Palindromic Substrings

Description:

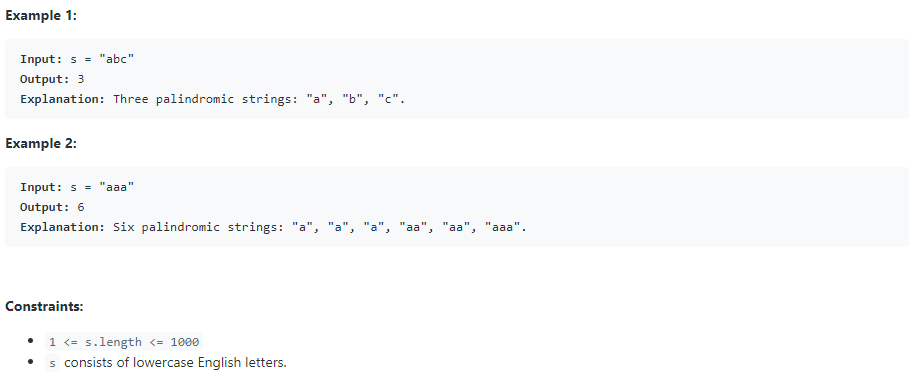
Given a string s, return the number of palindromic substrings in it.

A string is a palindrome when it reads the same backward as forward.

A substring is a contiguous sequence of characters within the string.

'''
[1] brute force)

code::
def countSubstrings(self, s: str) -> int:
    count=0
    for i in range(len(s)):
        for j in range(i,len(s)+1):
            if s[i:j]!="" and self.isPalindrome(s[i:j]):
                count+=1
    return count


def isPalindrome(self, s):
    left,right=0,len(s)-1

    while left<right:
        if s[left]!=s[right]:
            return False
        left+=1
        right-=1
    return True
       
-T/C: O(n^3)
-S/C: O(1)
'''
'''
[2] dynamic programming)

idea::
let, i is start index of substring, j is end index of substring ==> substring = s[i:j+1]
then, if s[i]==s[j] and s[i+1:right] is palindrome:
        s[i:j+1] is palindrome
so, make dp table

code::
def countSubstrings(self, s: str) -> int:
    # init dp table
    dp=[[0 for i in range(len(s))] for j in range(len(s))]

    for i in range(len(s)):
        dp[i][i]=1

    count=0

    # from dp_table' bottom to top
    for i in range(len(s)-1,-1,-1):
        for j in range(i,len(s)):
            if dp[i][j]==1:
                continue
            if s[i]==s[j]:
                if i+1>j-1:
                    dp[i][j]=1
                    count+=dp[i][j]
                elif dp[i+1][j-1]==1:
                    dp[i][j]=1
                    count+=dp[i][j]

    return count+len(s)

-T/C: O(n^2)
-S/C: O(n^2)
'''

class Solution:
    def countSubstrings(self, s: str) -> int:
        # init dp table
        dp=[[0 for i in range(len(s))] for j in range(len(s))]
        
        for i in range(len(s)):
            dp[i][i]=1
            
        count=0
        
        # from dp_table' bottom to top
        for i in range(len(s)-1,-1,-1):
            for j in range(i,len(s)):
                if dp[i][j]==1:
                    continue
                if s[i]==s[j]:
                    if i+1>j-1:
                        dp[i][j]=1
                        count+=dp[i][j]
                    elif dp[i+1][j-1]==1:
                        dp[i][j]=1
                        count+=dp[i][j]
                    
        return count+len(s)