62. Unique Paths
2021. 11. 17. 11:33ㆍLeetcode
Description:
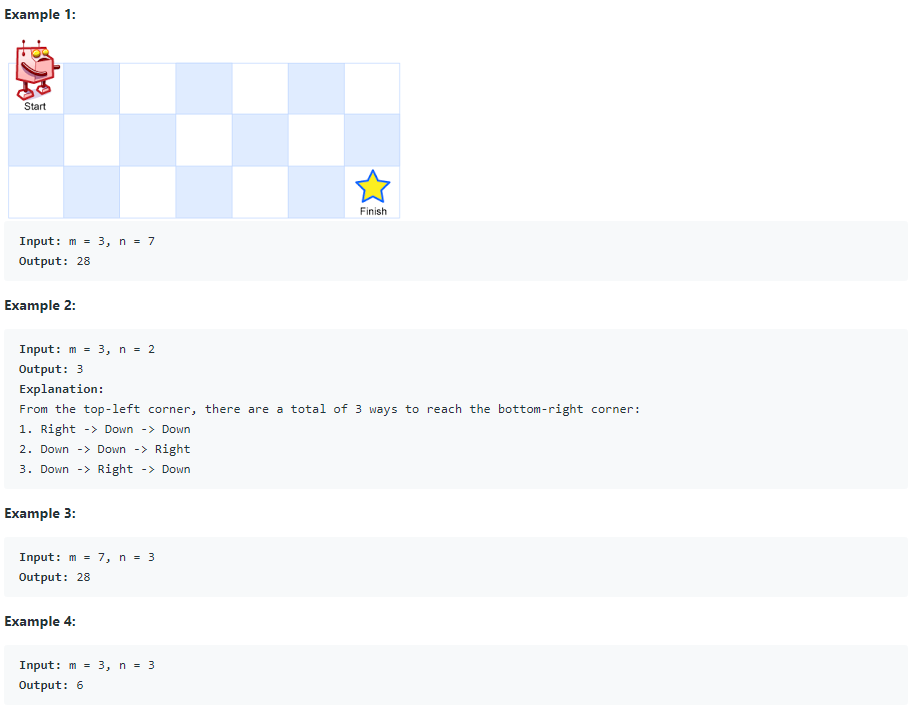
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?

'''
[1] dp)
idea::
paths[i][j]=path[i-1][j]+path[i][j-1]
code::
def uniquePaths(self, m: int, n: int) -> int:
paths=[[1 if i==0 or j==0 else 0 for j in range(n)] for i in range(m)]
for i in range(1,m):
for j in range(1,n):
paths[i][j]=paths[i-1][j]+paths[i][j-1]
return paths[m-1][n-1]
-T/C: O(m*n)
-S/C: O(m*n)
'''
'''
[2] dp - optimization)
idea::
not store whole matrix, just store past array
code::
def uniquePaths(self, m: int, n: int) -> int:
prev_paths=[1 for _ in range(n)]
for i in range(1,m):
cur_paths=[1 if i==0 else 0 for i in range(n)]
for j in range(1,n):
cur_paths[j]=cur_paths[j-1]+prev_paths[j]
prev_paths=cur_paths[:]
return prev_paths[-1]
-T/C: O(m*n)
-S/C: O(n)
'''
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
prev_paths=[1 for _ in range(n)]
for i in range(1,m):
cur_paths=[1 if i==0 else 0 for i in range(n)]
for j in range(1,n):
cur_paths[j]=cur_paths[j-1]+prev_paths[j]
prev_paths=cur_paths[:]
return prev_paths[-1]'Leetcode' 카테고리의 다른 글
| 208. Implement Trie (Prefix Tree) (0) | 2021.11.17 |
|---|---|
| 235. Lowest Common Ancestor of a Binary Search Tree (0) | 2021.11.17 |
| 230. Kth Smallest Element in a BST (0) | 2021.11.16 |
| 98. Validate Binary Search Tree (0) | 2021.11.16 |
| 297. Serialize and Deserialize Binary Tree (0) | 2021.11.15 |