931. Minimum Falling Path Sum
2021. 10. 16. 03:32ㆍLeetcode
Description:
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
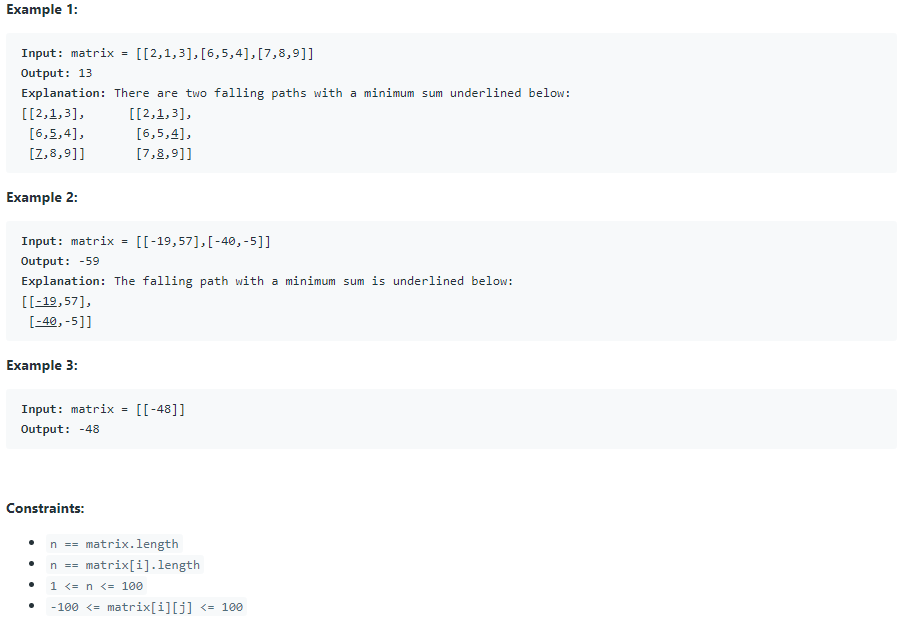
"""
[1] Brute Force)
def bf(mat,curRow,curSum):
if curRow==len(mat)-1:
return curSum
else:
i,j,k=infinite
when, left.possible():
i=bf(mat,curRow+1,curSum+left_value)
when, below.possible(): # always True
j=bf(mat,curRow+1,curSum+below_value)
when, right.possible():
k=bf(mat,curRow+1,curSum+right_value)
return min(i,j,k)
min=infinite
for i in range(len(mat)):
min=min(min,bf(mat,0,mat[0][i]))
return min
- T/C: O(3^n) # when supposing that left, right and below are always possible at every step
- S/C: O(1)
"""
"""
[2] Greedy)
idea: select the lowest value at the top, and then, again, select the lowest value in possible paths at the next row, and so on...
but, Greedy method is not accepted.
when,
[ 2, 0, -3 ]
[-7k, 6k, 5k ]
[-8k, 10k, 11k]
-3 + 5k + 10k = 15k-3
but, min falling path sum = 2-7k-8k = -15k+2
"""
"""
[3] DP - bottom up)
if denoting F([x][y])= min falling path when arrived at the matrix[x][y]
F([r][c])=min(F[r-1][c-1], F[r-1][c], F[r-1][c+1]) + path([r][c])
import copy
def dp(matrix):
# making dp matrix
dp=copy.deepcopy(matrix) # dp[0][0] ~ dp[0][n-1] are initialized
for row in range(1,len(matrix)):
for col in range(len(matrix[row])):
min_path=dp[row-1][col] # above
if col-1>=0: # if above-left possible
min_path=min(min_path,dp[row-1][col-1])
if col+1<len(matrix[row-1]): # if above-right possible
min_path=min(min_path,dp[row-1][col+1])
dp[row][col]=min_path + matrix[row][col]
# return minimum value at the last row
result=dp[len(matrix)-1][0]
for path_sum in dp[len(matrix)-1]:
result = min(result, path_sum)
return result
- T/C: O(n^2)
- S/C: O(n^2) # because I've made dp_matrix of the same size as matrix_input
"""
"""
[4] DP - optimization)
not making dp_mat, overwriting dp_mat values on the matrix
for row in range(1,len(matrix)):
for col in range(len(matrix[row])):
min_path=matrix[row-1][col] # above
if col-1>=0:
min_path=min(min_path,matrix[row-1][col-1])
if col+1<len(matrix[row-1]):
min_path=min(min_path,matrix[row-1][col+1])
matrix[row][col]=min_path + matrix[row][col]
result = matrix[len(matrix)-1][0]
for path_sum in matrix[len(matrix)-1]:
result=min(result, path_sum)
return result
- T/C: O(n^2)
- S/C: O(1)
"""
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
for row in range(1, len(matrix)):
for col in range(len(matrix[row])):
min_path=matrix[row-1][col]
if col-1>=0:
min_path=min(min_path,matrix[row-1][col-1])
if col+1<len(matrix[row-1]):
min_path=min(min_path,matrix[row-1][col+1])
matrix[row][col]+= min_path
result=matrix[len(matrix)-1][0]
for path_sum in matrix[len(matrix)-1]:
result=min(result,path_sum)
return result'Leetcode' 카테고리의 다른 글
| 661. Image Smoother (0) | 2021.10.17 |
|---|---|
| 73. Set Matrix Zeroes (0) | 2021.10.17 |
| 1155. Number of Dice Rolls With Target Sum (0) | 2021.10.16 |
| 3. Longest Substring Without Repeating Characters (0) | 2021.10.15 |
| 1008. Construct Binary Search Tree from Preorder Traversal (0) | 2021.10.15 |